W

Izometria, także przekształcenie izometryczne – funkcja, zachowująca odległości między punktami przestrzeni metrycznej. Jest to więc izomorfizm izometryczny. W geometrii figury, między którymi istnieje izometria, nazywane są przystającymi.

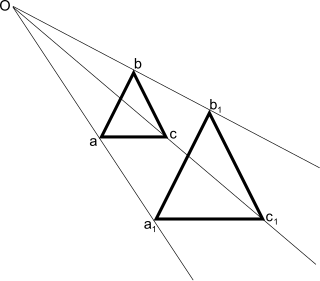
W

Jednokładność, homotetia o środku i niezerowej skali – odwzorowanie geometryczne prostej, płaszczyzny lub przestrzeni, określone następująco:

W

Przekształcenie afiniczne , powinowactwo lub pokrewieństwo – przekształcenie geometryczne przestrzeni euklidesowych, odwzorowujące odcinki na odcinki, proste w proste, płaszczyzny w płaszczyzny, linie równoległe w linie równoległe. Jednak w ogólności transformacja afiniczna nie zachowuje kątów między prostymi ani odległości między punktami, jednak zachowuje stosunki odległości między punktami na tej samej linii. Także transformacja afiniczna niekoniecznie zachowuje punkt początkowy przestrzeni wektorowej – w odróżnieniu od transformacji liniowej – dlatego każda transformacja liniowa jest afiniczna, ale nie odwrotnie.

W

Symetria osiowa – odwzorowanie geometryczne płaszczyzny lub przestrzeni, które dla ustalonej osi, tj. prostej, każdemu punktowi swojej dziedziny przyporządkowuje taki punkt że punkty i wyznaczają prostą przecinającą prostopadle oś i leżą w równej odległości od osi l po jej przeciwnych stronach. Symetrię względem osi oznacza się najczęściej jako

W

Symetria płaszczyznowa względem płaszczyzny P – odwzorowanie geometryczne przestrzeni przyporządkowujące każdemu punktowi A tej przestrzeni punkt A’ taki, że punkty A i A’ leżą na prostej prostopadłej do P, w równych odległościach od płaszczyzny P i po jej przeciwnych stronach. Punktami stałymi symetrii płaszczyznowej są punkty płaszczyzny P i tylko one.

W

Symetria środkowa o środku P – odwzorowanie geometryczne SP prostej, płaszczyzny lub przestrzeni takie, że SP(Q) = R wtedy i tylko wtedy, gdy punkt P, nazywany środkiem symetrii środkowej, jest środkiem odcinka QR. Punkty Q i R nazywa się punktami symetrycznymi względem środka symetrii P.

W

Symetria z poślizgiem – przekształcenie izometryczne płaszczyzny lub przestrzeni, będące przemiennym złożeniem symetrii i przesunięcia. Na płaszczyźnie symetria z poślizgiem sprowadza się do złożenia symetrii osiowej i przesunięcia o wektor równoległy do osi symetrii. W przestrzeni symetria z poślizgiem jest złożeniem symetrii płaszczyznowej i przesunięcia o wektor równoległy do płaszczyzny symetrii.

W

Translacja, przesunięcie – przekształcenie prostej, płaszczyzny lub dowolnej przestrzeni afinicznej, które można intuicyjnie rozumieć jako równoległe przesunięcie wszystkich punktów dziedziny bez jej deformacji i obracania.