29 Geometria euklidesowa

Geometria euklidesowa – klasyczna odmiana geometrii opisana po raz pierwszy przez Euklidesa w dziele Elementy. Zebrał on całą ówczesną wiedzę matematyczną znaną Grekom, dziś jego dzieło przedstawia się jako pierwszą znaną aksjomatyzację w historii matematyki. Pierwotnie uprawiano ją jedynie na płaszczyźnie i w przestrzeni trójwymiarowej wiążąc ją jednocześnie ze światem fizycznym, który miała opisywać, nie dopuszczając tym samym możliwości badania innych odmian geometrii.

Aksjomat Pascha – aksjomat płaszczyzny euklidesowej niedający się wyprowadzić z pięciu aksjomatów Euklidesa:Dane są na płaszczyźnie prosta i punkty i spoza takie, że odcinek przecina Jeśli jest kolejnym punktem poza to dokładnie jeden z odcinków lub przecina .

Diagram w greckiej geometrii – rysunek linii prostych i zazwyczaj też okręgów wraz z towarzyszącymi im symbolami literowymi, stanowiący integralną część przekazu geometrycznego w Elementach Euklidesa oraz w dziełach Archimedesa i innych greckich geometrów.

Elementy – pochodzący z końca IV wieku p.n.e. traktat geometryczny i arytmetyczny autorstwa Euklidesa, obejmujący swym zakresem podstawowe zagadnienia obu tych nauk.

Metoda graficzna obliczania pól – metoda obliczania pól powierzchni.

Metoda wyczerpywania (łac. methodus exhaustionibus) – metoda obliczania pola powierzchni figury geometrycznej za pomocą wpisania w nią ciągu wzajemnie rozłącznych wielokątów o znanej powierzchni, których suma pól zbliża się do powierzchni badanej figury.

Odcinek – część prostej zawarta pomiędzy dwoma jej punktami z tymi punktami włącznie. Odcinek w całości zawiera się wewnątrz tej prostej.

Odległość punktu (P) od prostej (k) jest to najmniejsza spośród odległości pomiędzy punktem P i punktami prostej k. Odległością tą jest długość odcinka prostej prostopadłej do k, którego końcami są punkt P i przecięcie z prostą k.

Okrąg – zbiór wszystkich punktów płaszczyzny euklidesowej odległych od ustalonego punktu, nazywanego środkiem, o zadaną odległość, nazywaną promieniem.

Okrąg Apoloniusza – zbiór punktów, dla których stosunek odległości od pewnych dwóch ustalonych punktów jest stały i różny od jeden. Nazwany tak na cześć Apoloniusza z Pergi, który badał krzywe stożkowe.

Okrąg dopisany do trójkąta – okrąg styczny do jednego z boków trójkąta i przedłużeń dwóch pozostałych boków. Jego środek znajduje się w punkcie przecięcia dwusiecznych odpowiednich kątów zewnętrznych. Okrąg ten ma dokładnie jeden punkt wspólny z trójkątem.

Okrąg Forda – okrąg o środku w punkcie o współrzędnych i promieniu równym oznacza tu liczbę wymierną zapisaną w postaci ułamka nieskracalnego.

Płaszczyzna zespolona – geometryczny model ciała liczb zespolonych Płaszczyzna pełni w nim w stosunku do liczb zespolonych rolę analogiczną do roli, którą pełni prosta rzeczywista względem ciała liczb rzeczywistych.

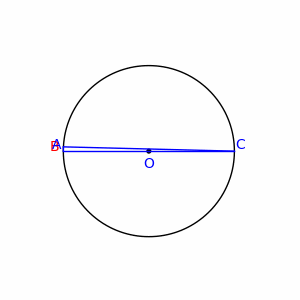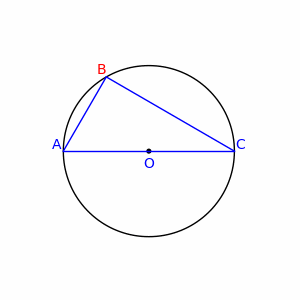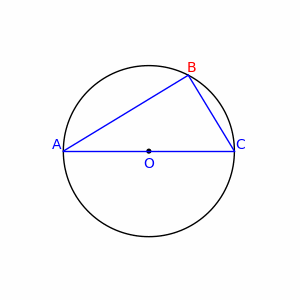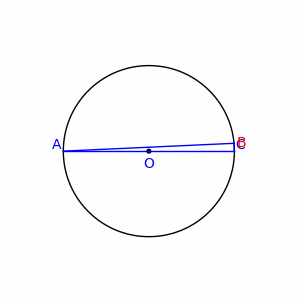
Potęga punktu względem okręgu – liczba równa gdzie jest środkiem okręgu jego promienieniem. Z definicji wynika, że dla punktu leżącego na zewnątrz okręgu. jest wtedy równe kwadratowi długości stycznej poprowadzonej z punktu do okręgu . dla punktu leżącego wewnątrz okręgu. jest liczbą przeciwną do kwadratu połowy najkrótszej cięciwy okręgu przechodzącej przez punkt . dla punktów leżących na okręgu.

Półokrąg – łuk okręgu wyznaczony przez kąt środkowy o mierze 180°. Końce półokręgu leżą więc na jednej średnicy. Promieniem półokręgu jest promień okręgu, którego częścią jest półokrąg.

Półprosta – figura geometryczna składająca się z punktów prostej leżących po jednej stronie pewnego punktu tej prostej. Punkt ten jest nazywany początkiem półprostej. Bardzo często do tak określonej półprostej dołącza się początek półprostej – mówimy wówczas o półprostej domkniętej. W przeciwnym wypadku mówimy o półprostej otwartej.

Problem Apoloniusza – problem matematyczny polegający na stworzeniu okręgu stycznego do trzech innych okręgów. Apoloniusz z Pergi przedstawił i rozwiązał ten problem w swojej pracy Ἐπαφαί ; praca ta zaginęła, jednak raport na temat jej wyników, który wykonał Pappus z Aleksandrii, przetrwał. Dla dowolnych trzech okręgów można stworzyć 8 różnych okręgów, które będą do nich styczne.

Problem Fagnana – problem optymalizacyjny postawiony po raz pierwszy przez włoskiego matematyka i duchownego Giovanniego Fagnana w 1775:Dla danego trójkąta ostrokątnego wyznaczyć trójkąt wpisany o minimalnym obwodzie.

Promień – odcinek łączący środek koła, okręgu, kuli lub sfery z dowolnym punktem położonym na jej brzegu, a także długość tego odcinka. Długość promienia jest w tym przypadku zawsze równa połowie długości średnicy, co wyraża wzór

Prosta potęgowa lub oś potęgowa – miejsce geometryczne punktów mających równe potęgi względem danych dwóch okręgów; inaczej: miejsce geometryczne punktów, w których styczne do dwóch danych okręgów mają tę samą długość. Środkiem potęgowym nazywa się punkt przecięcia co najmniej dwóch osi potęgowych.

Prostopadłość – relacja między dwiema prostymi, dwiema płaszczyznami lub prostą i płaszczyzną.Dwie proste są prostopadłe, gdy tworzą przystające kąty przyległe. Prosta i płaszczyzna są prostopadłe, gdy prosta jest prostopadła do każdej prostej przecinającej prostą i zawartej w płaszczyźnie . Dwie płaszczyzny i są prostopadłe, gdy istnieje prosta zawarta w płaszczyźnie i prostopadła do płaszczyzny .

Sieczna – prosta przecinająca daną krzywą w co najmniej dwóch punktach. Odcinek siecznej ograniczony punktami przecięcia z krzywą nazywa się cięciwą tej krzywej.

Sprzężenie izotomiczne punktu w trójkącie to inny punkt, określony jednoznacznie poprzez trójkąt oraz położenie punktu wyjściowego punktu.

Srebrny podział – stała matematyczna, której nazwa nawiązuje do złotego podziału. Podobnie jak ilorazy dwóch kolejnych liczb Fibonacciego zbiegają do odwrotności złotej liczby, tak odwrotność srebrnej liczby jest granicą ilorazów dwóch kolejnych liczb Pella. Dwa odcinki będące w srebrnym podziale mają się więc do siebie tak, jak bok jednostkowego kwadratu do jego przekątnej.

Symetralna odcinka – prosta prostopadła do danego odcinka przechodząca przez jego środek.

Vesica piscis – krzywa o migdałowatym kształcie, zamknięta na płaszczyźnie, symetryczna względem swojego środka, powstała w geometrii euklidesowej przez przecięcie się dwóch okręgów o równych promieniach w taki sposób, że środek jednego okręgu leży na okręgu drugim.

Wielokomórka (politop) – uogólnienie na dowolną liczbę wymiarów pojęcia wielokąta w drugim i wielościanu w trzecim wymiarze.

Złoty podział, podział harmoniczny, złota proporcja, boska proporcja – podział odcinka na dwie części tak, by stosunek długości dłuższej z nich do krótszej był taki sam, jak całego odcinka do części dłuższej. Innymi słowy: długość dłuższej części ma być średnią geometryczną długości krótszej części i całego odcinka. Rysunek obok ilustruje ten związek geometrycznie. Wyrażony algebraicznie: