 W
WFunkcja częściowa z do – funkcja gdzie jest podzbiorem .
 W
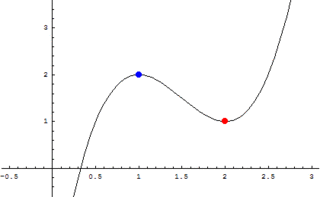
WEkstremum funkcji – maksymalna lub minimalna wartość funkcji.Funkcja przyjmuje w punkcie maksimum lokalne, jeśli w pewnym otwartym otoczeniu tego punktu funkcja nigdzie nie ma wartości większych. Jeśli dodatkowo w pewnym otwartym sąsiedztwie punktu funkcja nie ma również wartości równych to jest to maksimum lokalne właściwe. Minima i maksima lokalne są zbiorczo nazywane ekstremami lokalnymi. Największa i najmniejsza wartość funkcji w całej dziedzinie nazywane są odpowiednio maksimum i minimum globalnym, a zbiorczo ekstremami globalnymi.
 W
WFunkcja pierwotna – dla danej funkcji taka funkcja której pochodna jest równa Proces wyznaczania funkcji pierwotnej nazywa się również całkowaniem (nieoznaczonym) i można go postrzegać jako działanie odwrotne do wyznaczania pochodnej. Funkcje pierwotne, poprzez podstawowe twierdzenie rachunku całkowego, związane są z całkami oznaczonymi: całka oznaczona funkcji na danym przedziale jest równa różnicy wartości funkcji pierwotnej w końcach tego przedziału.
 W
WFunkcja prostokątna jest zdefiniowana jako
 W
WSignum, sgn – funkcja zmiennej rzeczywistej, zdefiniowana następująco:
 W
WFunkcja trójkątna jest zdefiniowana jako:
 W
WFunkcja holomorficzna – główny obiekt badań analizy zespolonej; funkcja zdefiniowana na otwartym podzbiorze płaszczyzny liczb zespolonych o wartościach w która jest różniczkowalna w sensie zespolonym w każdym punkcie tego podzbioru.
 W
WFunkcja monotoniczna – funkcja, która zachowuje określony rodzaj porządku zbiorów. Pojęcie powstałe pierwotnie na gruncie analizy zostało uogólnione na gruncie teorii porządku.
 W
WFunkcja „na” – funkcja przyjmująca jako swoje wartości wszystkie elementy przeciwdziedziny, tj. której obraz jest równy przeciwdziedzinie.
 W
WNiezmiennik , inaczej -niezmiennik – pojęcie matematyczne wprowadzone przez Kleina, definiowalne na dwa sposoby – czysto algebraiczny, związany z krzywymi eliptycznymi oraz analityczny, jako specyficzna funkcja modularna.
 W
WFunkcja ograniczona – funkcja, której wszystkie wartości należą do pewnego przedziału ograniczonego.
 W
WFunkcja przedziałami liniowa – funkcja zmiennej rzeczywistej, której dziedzina daje się rozbić na sumę rozłącznych przedziałów w ten sposób, że w każdym z nich funkcja jest liniowa.
 W
WFunkcja Riemanna – funkcja rzeczywista zdefiniowana wzorem:
 W
WFunkcja Rosenbrocka – funkcja niewypukła używana w optymalizacji jako test dla algorytmów optymalizacji. Zwana jest też ze względu na swój kształt „doliną Rosenbrocka” lub „funkcją bananową Rosenbrocka”.
 W
WFunkcja różnowartościowa – funkcja, której każdy element przeciwdziedziny przyjmowany jest co najwyżej raz.
 W
WFunkcja schodkowa – funkcja, która jest stała na określonych przedziałach. Intuicyjnie, jest to funkcja, której wykres przypomina schodki. Najbardziej znane funkcje schodkowe:Część całkowita Funkcja signum Funkcja skokowa Heaviside'a dystrybuanta dyskretnego rozkładu prawdopodobieństwa
 W
WFunkcja skokowa Heaviside’a, skok jednostkowy – funkcja nieciągła, która przyjmuje wartość dla ujemnych argumentów i wartość w pozostałych przypadkach:
 W
WFunkcja „w” – żargonowe określenie funkcji, która jako swoje wartości nie przyjmuje wszystkich elementów przeciwdziedziny, co zapisujemy:
 W
WFunkcja wzajemnie jednoznaczna a. bijekcja – funkcja, w której każdemu elementowi dziedziny odpowiada jeden i tylko jeden element przeciwdziedziny; wzajemnie jednoznaczna odpowiedniość między elementami dwóch zbiorów, czyli funkcja będąca jednocześnie funkcją różnowartościową (iniekcją) i funkcją „na” (surjekcją).