W

Algorytm Metropolisa-Hastingsa – metoda statystyczna typu MCMC, pozwalająca stochastycznie oszacowywać całki i rozkłady prawdopodobieństwa dla złożonych systemów, które są zbyt trudne do modelowania analitycznego, np. układów wielowymiarowych. Narzędzie to jest wykorzystywane między innymi we wnioskowaniu bayesowskim i modelowaniu systemów fizycznych. Procedurę opisał po raz pierwszy publicznie zespół Metropolisa w 1953 r., a rozwinął ją Hastings w 1970 r. Metody Monte Carlo tego rodzaju stosowali także Enrico Fermi i Stanisław Ulam w trakcie tajnych prac nad Projektem Manhattan.

W

Ekstrapolacja – prognozowanie wartości pewnej zmiennej lub funkcji poza zakresem, dla którego mamy dane, przez dopasowanie do istniejących danych pewnej funkcji, następnie wyliczenie jej wartości w szukanym punkcie.

W

Integraf – urządzenie do całkowania graficznego, wyspecjalizowany integrator; przy przesuwaniu wodzika wzdłuż danej krzywej sporządza wykres jej całki nieoznaczonej. W Polsce oryginalne integrafy zbudowali w XIX wieku Wawrzyniec Żmurko i Brunon Abakanowicz. Ten drugi opatentował urządzenie w 1880 i odtąd jego integraf był produkowany przez szwajcarskie przedsiębiorstwo Coradi.

W

LS-DYNA – pakiet oprogramowania do analizy zjawisk szybkozmiennych metodą elementów skończonych rozwijany przez amerykańską firmę Livermore Software Technology Corporation (LSTC) w Livermore w Kalifornii, wykorzystujący szybkie sformułowanie typu "explicit". LS-DYNA znajduje zastosowanie m.in. w przemyśle samochodowym, lotnictwie, astronautyce, budownictwie, przemyśle maszynowym, wojskowości i bioinżynierii. Pierwowzorem oprogramowania LS-DYNA był program DYNA3D, opracowany w 1976 roku przez dr. Johna O. Hallquista z Lawrence Livermore National Laboratory w celu modelowania wybuchów bomb jądrowych.

W

Macierz rzadka – macierz, w której większość elementów ma wartość zero.

W

Metoda elementów skończonych, MES – zaawansowana metoda numerycznego rozwiązywania problemów brzegowych. Polega ona na zastosowaniu interpolacji poszukiwanej funkcji, na dyskretnym zbiorze jej węzłów, które powstają w wyniku dyskretyzacji dziedziny jej określoności na tzw. elementy skończone.

W

Metoda gradientu sprzężonego jest algorytmem numerycznym służącym do rozwiązywania niektórych układów równań liniowych. Pozwala rozwiązać te, których macierz jest symetryczna i dodatnio określona. Metoda gradientu sprzężonego jest metodą iteracyjną, więc może być zastosowana do układów o rzadkich macierzach, które mogą być zbyt duże dla algorytmów bezpośrednich takich jak np. rozkład Choleskiego. Takie układy pojawiają się często w trakcie numerycznego rozwiązywania równań różniczkowych cząstkowych.

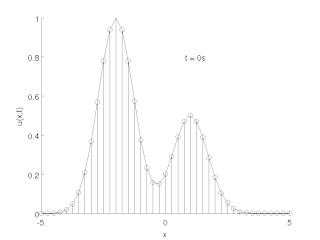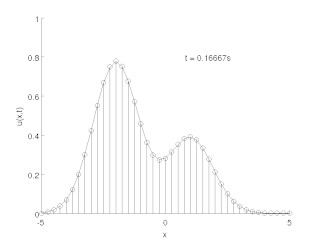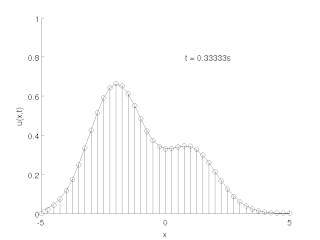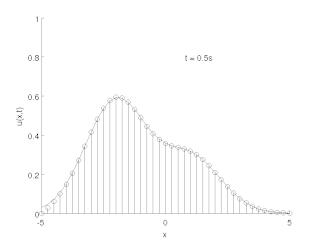
W

Metoda linii – technika numerycznego rozwiązywania równań różniczkowych cząstkowych. Polega ona na dyskretyzacji przestrzennej danego równania, co prowadzi do układu równań różniczkowych zwyczajnych na siatce przestrzennej, który można scałkować względem czasu za pomocą szeroko dostępnych metod numerycznych.

W

Metoda Monte Carlo (MC) – metoda stosowana do modelowania matematycznego procesów zbyt złożonych, aby można było przewidzieć ich wyniki za pomocą podejścia analitycznego. Istotną rolę w tej metodzie odgrywa losowanie wielkości charakteryzujących proces, przy czym losowanie dokonywane jest zgodnie z rozkładem, który musi być znany.

W

Metoda poziomic – numeryczna metoda pozwalająca na śledzenie hiperpowierzchni ewoluującej pod wpływem pewnego pola prędkości zdefiniowanego w jej punktach, bez konieczności parametryzowania tej hiperpowierzchni. Jest to możliwe dzięki rezygnacji z jawnej reprezentacji hiperpowierzchni (explicit) kosztem reprezentacji implicit, gdzie funkcja ta reprezentowana jest poprzez zbiór swoich wartości w punktach węzłowych siatki kartezjańskiej zdefiniowanej w interesującym nas obszarze przestrzeni.

W

Całkowanie metodą Simpsona – jedna z metod przybliżania wartości całki oznaczonej funkcji rzeczywistej.

W

MPSolve – program do numerycznego obliczania miejsc zerowych wielomianów jednej zmiennej. Używa metody Abertha.

W

Optymalizacja – problem polegający na znalezieniu ekstremum zadanej funkcji celu.

W

Propagacja błędu, propagacja niepewności, przenoszenie się błędu – statystyczne zjawisko występujące w operacjach dokonywanych na wartościach obarczonych błędem, np. błędem pomiaru.

W

Próbkowanie Monte Carlo łańcuchami Markowa – klasa algorytmów próbkowania z rozkładu prawdopodobieństwa. Poprzez budowę łańcucha Markowa, który ma rozkład równowagowy taki jak szukana dystrybucja, można wydajnie próbkować złożone rozkłady prawdopodobieństwa. Im większa liczba kroków w takim algorytmie, tym dokładniej rozkład próbki odpowiada pożądanemu rozkładowi.

W

Przybliżenie Padégo – metoda aproksymacji funkcji za pomocą funkcji wymiernych danego rzędu. Często daje lepszy wynik niż szereg Taylora dla tej samej liczby współczynników, kiedy funkcja posiada bieguny.

W

Warunek Couranta-Friedrichsa-Lewy’ego – matematyczny warunek zbieżności numerycznych metod rozwiązywania pewnych równań różniczkowych cząstkowych. Pojawia się przy analizie stabilności jawnych metod numerycznych dla zagadnień zależnych od czasu.

W

Wzór Boole’a – jedna z metod całkowania numerycznego, której nazwa wywodzi się od nazwiska Angielskiego matematyka George’a Boole’a. Często błędnie podawany jako wzór Bode’a w wyniku błędu literowego występującego w publikacji „Abramowitz and Stegun” z roku 1964. Nowsze prace prawidłowo podają ów wzór jako „Boole’a” nie „Bode’a”.

W

Wzór trapezów – jeden z wzorów służących do przybliżonego obliczania całek oznaczonych w sensie Riemanna. Idea wzoru opiera się na geometrycznej interpretacji całki oznaczonej z funkcji nieujemnej jako pola pod wykresem funkcji.